15 Diatonic Modes
Mark Gotham and Megan Lavengood
Key Takeaways
- Church modes originated in the medieval era, and are classified by their use of the diatonic collection, their final, the relationships of other pitches to that final, and their range.
- In the 20th and 21st centuries, diatonic modes are also understood as rotations of the major scale, without range requirements, but with the concept of a pitch-class center or tonic.
- Non-Western musical cultures have their own methods of organizing pitch into modes. These “modes” are usually more than simple pitch collections and can include characteristic gestures, embellishments, and protocols for use. Examples include Indian raga, Arabic maqam, Balinese pelog and slendro, Jewish prayer modes, Persian dastgah, and Japanese scales.
- Modes, conceived in terms of parallel relationships, with an emphasis on the color notes of each mode:
- Ionian: Identical to major
- Mixolydian: Like major with a
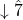
- Lydian: Like major with a
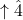
- Aeolian: Identical to natural minor; no raised leading tone
- Dorian: Like natural minor with a
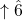
- Phrygian: Like natural minor with a
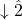
- Modes, conceived in terms of relative relationships:
- Ionian: White notes starting on C
- Dorian: White notes starting on D
- Phrygian: …starting on E
- Lydian: …starting on F
- Mixolydian: …starting on G
- Aeolian: …starting on A
This book covers modes from many different angles. For more information on modes, check Introduction to Diatonic Modes (general), Chord-Scale Theory (jazz), Modal Schemas (pop), and Analyzing with Modes, Scales, and Collections (20th-/21st-c.).
At the turn of the 20th century, many composers were rethinking the materials of music. This is one reason the term “common practice” is used to distinguish the major-minor music that dominated Western classical music for the 200 years or so prior—something changed around 1900. You’ll also hear talk of the “emancipation of the dissonance” connected to this, and the emergence of atonality out of ever-more-radical chromatic maneuvers. The history of music is much more complex than this simple take, but there is some truth to it: a lot of composers were interested in reinventing what and how they composed, similar to the emergence of abstract art around the same time.
The use of modes has a place in all of this, encapsulating many of the ways in which one can broaden the compositional palette. In this chapter, we’ll go through some of the most interesting, famous, and significant options, starting, as many composers did, by looking back to what came before.
Church Modes
The dominance of major and minor in Western classical music emerged out of an earlier practice centered on the use of modes. This collection of modes is often called church, white-note, or Gregorian modes. These modes correspond to rotations of the C major scale, using the same collection of pitches but a different tonic (more properly referred to as a final in this context).
This already introduces us to a fundamental tenet of what a mode generally comprises: both a diatonic collection of pitches and a final. These are the first two items on the list below, followed by two other particularly useful concepts for understanding church modes:
- The diatonic collection and the intervallic relationships between those pitches
- The final, which acts as a referential point
- Further hierarchical levels between the pitch in the mode and its final
- Melodic shapes and range
1–3 will be familiar from tonal music, but 4 may not be. Range is a defining characteristic of the church modes, as each mode has an authentic and a plagal version.
Example 1 summarizes the modes by their final, their tenor, and their range. Authentic modes are on the left, while plagal modes (those beginning with “hypo-“) are on the right. Tenors are usually a fifth above the final in authentic modes and a third above the final in plagal modes (except where noted with an exclamation point). Example 2 provides the same summary, but in notation.
[table “81” not found /]
Example 1. The historical church modes summarized.
Example 2. The historical church modes summarized in notation.
Diatonic Modes in the 20th and 21st centuries
Another summary of diatonic modes (and assignments on them) can be found in Introduction to Diatonic Modes and the Chromatic “Scale.”
When modes were revisited as a compositional concept in the 20th century, many concepts from church modes were maintained, while other distinctions were erased. The notion of authentic/plagal modes (“hypo-” modes) was dropped, as the range of many pieces spans more than one octave. Additionally, Glarean’s later modes, aeolian and ionian, were just as important as the original authentic church modes.
Color notes
As a listener, you may experience modes as sounding similar to major or minor, but with certain inflected notes—color notes.[1] Modes will sound major-ish or minor-ish based on the quality of the third above the tonic. The major-ish modes are mixolydian and lydian; the minor-ish modes are aeolian, dorian, and phrygian.
Example 3 lists each mode, the quality of the third above the tonic, its color note that distinguishes it from major/natural minor, and its pitches parallel and relative to C major.
[table “30” not found /]
Example 3. Important characteristics of each mode.
Example 4 provides a brief summary of this information using notation. The modes are grouped by whether the tonic is major or minor, which helps with aural identification of modal passages (as discussed further below). The top line shows modes whose 
is a major third above tonic (mi): major, mixolydian, and lydian. The bottom line shows modes whose is a minor third above tonic (me): aeolian, dorian, and phrygian. The dotted slurs connect the distinctive color note of each mode with its major/minor counterpart.
Example 4. Modes grouped by major vs. minor tonic, with color notes shown in blue.
Hearing modal tonics
Because many listeners are so enculturated to hear all music as being major or minor, 20th and 21st century composers who wish to create a modal sound will often spend extra energy on emphasizing the tonic pitch of their chosen mode. (Note that this may or may not involve emphasizing a tonic chord!) Following are several ways in which composers may create a sense of tonic in modal music.
- repeating the tonic pitch
- agogic accents (using longer note values) on the tonic pitch, including using a drone of the tonic pitch
- metrical accents on the tonic pitch
- using the tonic pitch as the lowest pitch
- cadencing on the tonic pitch
Identifying modes
If you are not used to playing in and listening to modes, it can be daunting to identify and distinguish modes. Here is a step-by-step process for distinguishing all the modes discussed here, illustrated as a flowchart in Example 5.
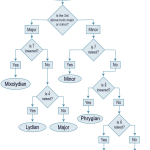
1. Identify the quality of tonic.
Listen for the tonic pitch. Then, listen for the whole tonic chord. Is the third of that chord major or minor? This distinguishes the major-ish modes (major, mixolydian, lydian) from the minor-ish modes (minor, aeolian, dorian).
2. Listen and look for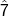 
(ti or te).
Compare the 
to the leading tone (ti) a half step below tonic that we typically hear in minor and major pieces. If is a whole step below tonic (te), then it’s lowered, which means that the piece is (at least temporarily) in a mode.
If you heard a major tonic and is lowered (te), then you are in mixolydian.
If you heard a minor tonic and is raised (ti), then you are in minor.
If your mode is not already identified, proceed to step 3.
3. Listen and look for other color notes— fi (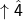
) in major, la (
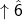) in minor, or ra 
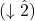in minor.
If did not identify the mode for you, listen and look for other raised color notes.
If 
is raised (fi) in a major-tonic mode, you are in lydian. If it is not, you are in major.
If 
is lowered (ra) in a minor-tonic mode, you are in phrygian. If 
is raised (la) in a minor-tonic mode, you are in dorian. If neither 
nor is altered (te, le, re), you are in aeolian.
Modes in a Global Context
Almost all cultures in any place and time have had music, and the vast majority of them have organized pitch into what Western music theory considers types of modes. So, as you might imagine, there are a lot of options for composers prepared to look out beyond the Western tradition to explore. Around 1900, composers in Europe and North America began to do just that. Composers drew on music of the African diaspora (which would come to exert a huge influence over all forms of music making in the 20th century), the ancient ragas of India, China, the Balkans, and many more besides. Clearly, there’s no way we can do justice to such a huge topic here—nor indeed could 20th-century Western classical music, which often flattened out nuances of these complex systems. Following is an incomplete list of non-European sources of mode-like pitch collections:
- Indian raga
- Arabic maqam and Turkish makam
- Balinese pelog and slendro
- Jewish prayer modes
- Persian dastgah
- Japanese scales
Each of these systems of pitch organization is related to the concept of mode discussed here, but each has nuances and practices that distinguish them from the diatonic modes, even if the pitches are identical.
- Persichetti, Vincent. 1961. Twentieth-Century Harmony. New York: W. W. Norton.
- Identifying modes (.pdf, .mscz). Asks students to identify 20th-century modes versus major/minor, circle inflected pitches, and explain how a pitch center is articulated. Music examples are transcribed from the TV show Great British Bake Off (music by Tom Howe, © Accorder Music Publishing, used with permission). Worksheet playlist
- Additional beginner’s worksheets can be found in Introduction to Diatonic Modes and the Chromatic “Scale.”
- Vincent Persichetti (1961) referred to these notes as "characteristic notes." ↵
Key Takeaways
- Two pitches form an interval, which is usually defined as the distance between two notes.
- Melodic intervals are played or sung separately, while harmonic intervals are played or sung together.
- Every interval has a size and a quality. An interval's size is the distance between two notes on a staff—i.e., it is a measurement of the number of lines and spaces between two notes.
- Interval size is considered generic. In other words, it doesn't matter what accidentals you apply to the notes, the size is always the same.
- A quality makes an interval specific when used in combination with a size. Unisons, fourths, fifths, and octaves form perfect intervals, while seconds, thirds, sixths, and sevenths form major and minor intervals.
- Any interval can be augmented or diminished. Augmented intervals are one half step larger than a perfect or major interval. Diminished intervals are one half step smaller than a perfect or minor interval.
- Intervals between a unison and an octave are called simple intervals. Any interval larger than an octave is a compound interval.
- Intervallic inversion occurs when two notes are "flipped." When you need to identify an interval where the lower note is the tonic of a difficult or imaginary major key, inverting the interval can help.
- Consonant intervals are intervals that are considered more stable, as if they do not need to resolve, while dissonant intervals are considered less stable, as if they do need to resolve.Two pitches form an interval, which is usually defined as the distance between two notes.
Two pitches form an interval, which is usually defined as the distance between two notes. But what does an interval measure? Physical distance on the staff? Difference in wavelength between pitches? Something else? Music theorists have had contradictory ideas on the definition of "interval," and these definitions have varied greatly with milieu. This chapter will focus on intervals as a measure of two things: written distance between two notes on a staff, and an aural "distance" (or space) between two sounding pitches. It will be important to keep in mind at all times that intervals are both written and aural, so that you are thinking of them musically (and not simply as an abstract concept that you are writing and reading).
Size
Intervals can be melodic (played or sung separately) or harmonic (played or sung together). In Example 1, the notes in the first measure sound together (harmonically), while in the second measure, they sound separately (melodically).
Example 1. A harmonic and a melodic interval.
Every interval has a size and a quality. A size is the distance between two notes on a staff—i.e., it is a measurement of the number of lines and spaces between two notes. Sizes are written with Arabic numbers (2, 3, 4, etc.); however, they are spoken with ordinal numbers (second, third, fourth, fifth, sixth, seventh, etc.). Always begin with "one" when counting size. Example 2 shows the eight sizes within a C major scale. As you can see, the sizes are labeled with ordinal numbers, with two exceptions: the interval between two notes on the same line or space is called a “unison,” not a “first,” and notes eight lines and spaces apart are said to be an “octave,” not an “eighth.”
Example 2. Sizes of intervals.
Size is considered generic. In other words, it doesn't matter what accidentals you apply to the notes—the size is always the same. Example 3 demonstrates this: despite the different accidentals, each of these intervals is a third (or “generic third”) because there are three lines/spaces between the two notes.
Example 3. Accidentals do not affect an interval’s generic size.
Quick tip for determining interval sizes:
- Odd numbered intervals (3rds, 5ths, 7ths, 9ths) will appear on the staff as either line to line or space to space.
- Even numbered intervals (2nds, 4ths, 6ths, Octaves) will appear on the staff as either line to space or space to line.
Once you have this information, it becomes fairly easy to spot interval size without having to count.
You can practice identifying interval size with the following exercise:
Perfect, Major, and Minor Qualities
A quality makes an interval specific when used in combination with a size. Quality more precisely measures written distance between notes, and—in combination with an interval's size—it describes the aural sound of an interval.
There are five possible interval qualities:
- Augmented (designated as A or +)
- Major (ma)
- Perfect (P)
- Minor (mi)
- Diminished (d or o)
The quality comes before the size when saying or writing an interval. For example, an interval could be described as a "perfect fourth" (abbreviated P4), a "minor third" (abbreviated mi3), or an "augmented second" (abbreviated A2 or +2).
For now, we will only discuss three qualities: perfect, major, and minor. Different theorists (in different locations and time periods) have applied these qualities to different sizes of intervals, depending on milieu. Example 4 shows how these qualities are applied today. The left column shows that seconds, thirds, sixths, and sevenths are major and/or minor, while the right column shows that unisons, fourths, fifths, and octaves are perfect intervals.
| Major/Minor | Perfect |
|---|---|
| 2nds | Unisons |
| 3rds | 4ths |
| 6ths | 5ths |
| 7ths | Octaves |
Example 4. Interval qualities.
The Major Scale Method for Determining Quality
There are several different methods for learning to write and identify qualities of intervals. One method you may have heard of is counting half steps. We do not recommend this method, because it is time consuming and often inaccurate. Instead, we recommend using what you know about major scales to identify interval quality.
To identify an interval (size and quality) using the major scale method you need to "think in the key" of one of the pitches in the interval. Keep in mind the following ideas:
In any given major key signature, every interval above the tonic is either major or perfect.
In any given major key signature, every interval below the tonic is either minor or perfect.
With this knowledge you can determine interval quality:
- Determine size (by counting lines and spaces between the notes or using the visual odd and even interval method described above).
- Imagine that one of the pitches of the interval is the tonic of a major scale. It doesn't matter whether this pitch is the upper or lower pitch as long as you remember which pitch you chose. This may be easier if the pitch you choose is in a key with very few accidentals such as C, G, F, D or B♭
- Determine whether or not the other note is in the major scale (imagined in step 2) and assign the corresponding quality.
- If the pitch is in the key:
- the interval is perfect (if it is a unison, fourth, fifth, or octave above or below the chosen tonic),
- major (if it is a second, third, sixth, or seventh above the chosen tonic), and
- minor (if it is a second, third, sixth or seventh below the chosen tonic).
- If it is not in the key: the interval could be minor (a lowered second, third, sixth, or seventh), or it could be augmented or diminished, which will be covered in the next section.
Example 5 shows two intervals. Try identifying their size and quality:
Example 5. Two intervals.
In Example 5a, the notes are F and C in treble clef. Here is how you would use the “Major Scale” method to identify the interval:
- First, this interval is a generic fifth (F to itself is 1; to G is 2; to A is 3; to B is 4; to C is 5).
- Second, C is within the key of F major (which has one flat, B♭).
- Therefore, the interval is a perfect fifth.
Let's now use this process for Example 5b. The notes in this example are E♭ and C♭ in treble clef. Let’s go through the same process again:
- First, this interval is a generic sixth (E♭ to itself is 1; to F is 2; to G is 3; to A is 4; to B is 5; to C is 6).
- Second, C♭ is not in the key of E♭ major (which has three flats: B♭, E♭, and A♭).
- Therefore, this is a minor sixth. If it were a major sixth, then the C would have to be C♮ instead of C♭, because C♮ is in the key of E♭ major.
You can practice identifying perfect, major, and minor intervals with the following exercise:
Augmented and Diminished Qualities
To review, there are five possible interval qualities, of which we have covered major, minor, and perfect:
- Augmented (designated as A or +)
- Major (ma)
- Perfect (P)
- Minor (mi)
- Diminished (d or o)
Augmented intervals are one half step larger than a perfect or major interval. The first measure of Example 6a first shows the notes F and C, which form a perfect fifth (because C is in the key of F major). The top note of this interval is then raised by a half step to a C♯, making the interval one half step larger. The interval from F to C♯ is therefore an augmented fifth (abbreviated as either A5 or +5). In the second measure of Example 6a, the first interval is a major sixth between G and E (because E is in the key of G major). The top note is then raised by a half step to E♯, making the interval into an augmented sixth (A6 or +6).
The bottom note of an interval can be altered as well. In the first measure of Example 6b, the perfect fifth F–C is turned into an augmented fifth by lowering the F by a half step to F♭, which makes the interval one half step larger than a perfect fifth. In the second measure of Example 6b, the major sixth G–E is turned into an augmented sixth by lowering the G by a half step to G♭.
Example 6. Augmented intervals created by (a) raising the top note and (b) lowering the bottom note.
Diminished intervals are one half step smaller than a perfect or minor interval. In the first measure of Example 7a, the perfect fifth F–C is made a half step smaller by lowering the top note to C♭, forming a diminished fifth (also called a tritone, usually abbreviated as d5 or o5). In the second measure, G–E form a major sixth, which becomes a minor sixth when the top note is lowered by a half step. The minor sixth then becomes a diminished sixth when the top note is lowered again to E𝄫. Note that contracting an interval by one half step turns perfect and minor intervals into diminished intervals, but it turns major intervals into minor intervals.
Again, it is not always the top note that is altered. In Example 7b, the perfect fifth F–C becomes diminished when the bottom note moves up a half step to F♯. In the second measure, the major sixth G–E first becomes a minor sixth when the G moves up a half step to G♯. This minor interval then becomes diminished when the G♯ moves to G𝄪 in the third measure, further contracting the interval by another half step.
Example 7. Diminished intervals created by (a) lowering the top note and (b) raising the bottom note.
Example 8 again demonstrates and summarizes the relative size of intervals. Each bracket in this example is one half step larger or smaller than the brackets to its right and left. In Example 8a, the interval quality is changed by altering the top note with accidentals. As you can see, intervals one half step larger than perfect or major intervals are augmented; intervals one half step smaller than major intervals are minor; and intervals one half step smaller than perfect or minor intervals are diminished. Example 8b outlines the same qualities as 10a, only with the bottom note altered by accidentals instead of the top note.
Example 8. Relative size of intervals with (a) the top note altered and (b) the bottom note altered.
If you find yourself having trouble visualizing the qualities of intervals with accidentals on the staff, it may help to think of the interval kinesthetically. For example, in Example 8a you can put one of your hands over the other (parallel to one another) and move your top hand up or down to reflect the change in quality. You can do the same thing in Example 8b, except you would move your bottom hand up and down. Remember that even though your hands may be moving closer together and further apart, the generic size of the interval remains the same; your hands are representing the changes of quality that occur when accidentals are added, changed, or removed.
You can practice identifying augmented and diminished intervals with the following exercise:
Doubly and Triply Augmented and Diminished Intervals
Intervals can be further contracted or expanded outside of the augmented and diminished qualities. An interval a half step larger than an augmented interval is a doubly augmented interval, while an interval a half step larger than a doubly augmented interval is a triply augmented interval. Likewise, an interval a half step smaller than a diminished interval is a doubly diminished interval, while an interval a half step smaller than a doubly diminished interval is a triply diminished interval.
Compound Intervals
The intervals discussed above, from unison to octave, are simple intervals, which have a size of an octave or smaller. Any interval larger than an octave is a compound interval. In Example 9, the notes A and C first form a minor third (a simple interval). When the C is brought up an octave in the second pair of notes, the interval becomes a minor tenth (a compound interval). Quality remains the same for simple intervals and their corresponding compound intervals.
If you want to make a simple interval a compound interval, add 7 to its size. Consequently:
- Unisons (which get the number 1) become octaves (8s)
- 2nds become 9ths
- 3rds become 10ths
- 4ths become 11ths
- 5ths become 12ths
- 6ths become 13ths
Conversely, if you wish to simplify a compound interval, as long as the compound interval is a 15th or smaller, you can subtract 7 from the compound interval to come up with the simplified interval.
- 13ths become 6ths
- 12ths become 5ths
- 11ths become 4ths
- 10ths become 3rds
- 9ths become 2nds
- Octaves become unisons
These are the most common compound intervals that you will encounter in your music studies. Remember that octaves, 11ths, and 12ths are perfect like their simple counterparts, while 9ths, 10ths, and 13ths are major/minor.
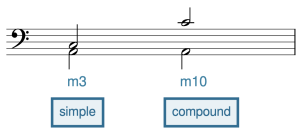
Intervallic Inversion
Intervallic inversion occurs when two notes are "flipped." In Example 10, for instance, an interval with C on the bottom and E on the top is inverted by moving the C up by an octave. You might be wondering: why is this important? There are two reasons: first, because inverted pairs of notes share many interesting properties (which are sometimes exploited by composers), and second, because inverting a pair of notes can help you to identify or write an interval when you do not want to work from the given bottom note.
Rule of Nine
Let's start with the first point: the interesting properties. First, the size of inverted pairs always adds up to 9:
- Unisons (1s) invert to octaves (8s) (1 + 8 = 9) and octaves invert to unisons.
- Seconds invert to sevenths (2 + 7 = 9) and sevenths invert to seconds.
- Thirds invert to sixths (3 + 6 = 9) and sixths invert to thirds.
- Fourths invert to fifths (4 + 5 = 9) and fifths invert to fourths.
Qualities of inverted pairs of notes are also very consistent:
- Perfect intervals invert to perfect intervals.
- Major intervals invert to minor intervals (and minor intervals to major intervals).
- Augmented intervals invert to diminished intervals (and diminished intervals to augmented intervals).
With that information, you can now calculate the inversions of intervals without even looking at staff paper. For example: a major seventh inverts to a minor second, an augmented sixth inverts to a diminished third, and a perfect fourth inverts to a perfect fifth.
Now for the second point: sometimes you will come across an interval that you do not want to calculate or identify from the bottom note. In the interval E𝄫–A♭ written in Example 11, for instance, identifying the interval using the “Major Scale” method would not work—the bottom note is E𝄫, and there is no key signature for this note (its key signature is “imaginary”). So, if you were given this interval to identify, you might consider inverting the interval. Now the inversion of the interval can be calculated from the non-imaginary key of A♭ major. The key of A♭ major has four flats (B♭, E♭, A♭, and D♭). An E♭ above A♭ would therefore be a perfect fifth; however, this interval has been contracted (made a half step smaller) because the E♭ has been lowered to E𝄫. That means this interval is a d5 (diminished fifth).
Now that we know the inversion of the first interval is a d5, we can calculate the original interval. A diminished fifth inverts to an augmented fourth (because diminished intervals invert to augmented intervals and because five plus four equals nine). Thus, the first interval is an augmented fourth (A4).
Consonance and Dissonance
Intervals are categorized as consonant or dissonant. Consonant intervals are intervals that are considered more stable, as if they do not need to resolve, while dissonant intervals are considered less stable, as if they do need to resolve. These categorizations have varied with milieu. Example 12 shows harmonically consonant and dissonant intervals:
| Melodically Consonant | Melodically Dissonant |
|---|---|
| Perfect Intervals | Augmented Intervals |
| ma2, mi2 | Diminished Intervals |
| ma3, mi3 | ma7, mi7 |
| ma6, mi6 |
Example 12. Melodically consonant and dissonant intervals.
Example 13 shows harmonically consonant and dissonant intervals:
| Harmonically Consonant | Harmonically Dissonant |
|---|---|
| ma3, mi3 | ma2, mi2 |
| ma6, mi6 | Augmented Intervals |
| P1, P8, P5 | Diminished Intervals |
| ma7, mi7 | |
| P4 |
Example 13. Harmonically consonant and dissonant intervals.
The implications of consonant and dissonant intervals are discussed further in the Introduction to Species Counterpoint.
Another Method for Intervals: The White-Key Method
Ultimately, intervals need to be committed to memory, both aurally and visually. There are, however, a few tricks to learning how to do this quickly. One such trick is the so-called "white-key method," which refers to the piano keyboard.
This method requires you to memorize all of the intervals found between the white keys on the piano (or simply all of the intervals in the key of C major). Once you’ve learned these, any interval can be calculated as an alteration of a white-key interval. For example, we can figure out the interval for the notes D and F♯ if we know that the interval D to F is a minor third and this interval has been made one semitone larger: a major third.
Conveniently, there is a lot of repetition of interval size and quality among white-key intervals, summarized in Example 14. Memorize the most frequent type and the exceptions.
- All of the seconds are major except for two: E–F and B–C.
- All of the thirds are minor except for three: C–E, F–A, and G–B, which are major.
- All of the fourths are perfect except for one: F–B, which is an augmented fourth (a tritone).
Example 14. White-key seconds, thirds, and fourths.
Believe it or not, you now know all of the white-key intervals, as long as you understand the concept of intervallic inversion, which was previously explained. For example, if you know that all seconds are major except for E–F and B–C (which are minor), then you know that all sevenths are minor except for F–E and C–B (which are major), as seen in Example 15.
Once you’ve mastered the white-key intervals, you can figure out any other interval by taking into account any accidentals applied to the notes.
A Variation of the White Key Method: Natural Intervals (Intervals without Accidentals)
This method relies on your ability to remember where the natural half steps fall on the piano keyboard or on the staff. The natural half steps are B-C and E-F. It is nearly identical to the white key method, but is explained slightly differently.
- 2nds - All major, except for B-C and E-F – those are the natural half steps, and are therefore minor. A Major 2nd is the same thing as a whole step. A minor 2nd is the same thing as a half step.
- 3rds - Natural 3rds that contain the natural half steps (B-C or E-F) will always be minor. All the other natural 3rds are Major.
- 4ths - All natural 4ths except F-B contain one of the natural half steps and are perfect. Since F-B contains neither of the natural half steps, it is augmented.
- 5ths - All natural 5ths except B-F contain one of the natural half steps and are perfect. Since B-F contains 2 natural half steps it is diminished.
- 6ths and 7ths - If a 6th or 7th contains one of the natural half steps, it is major. If it contains 2 of the natural half steps, it is minor.
And, as above, once you know the natural interval, you can figure out the quality by taking into account any accidentals (both in the key signature and on individual pitches) that alter the interval.
Intervallic Enharmonic Equivalence
Example 16 may be useful when thinking about enharmonic equivalence of intervals. In this chart, the columns are different intervallic sizes, while the rows present intervals based on the number of half steps they contain. Each row in this chart is enharmonically equivalent. For example, a major second (ma2) and diminished third (d3) are enharmonically equivalent (both are two half steps). Likewise, an augmented fourth (A4) and diminished fifth (d5) are enharmonically equivalent—both are six half steps in size.
| number of semitones | unis. | 2nd | 3rd | 4th | 5th | 6th | 7th | oct. |
|---|---|---|---|---|---|---|---|---|
| 0 | P1 | d2 | ||||||
| 1 | A1 | mi2 | ||||||
| 2 | ma2 | d3 | ||||||
| 3 | A2 | mi3 | ||||||
| 4 | ma3 | d4 | ||||||
| 5 | A3 | P4 | ||||||
| 6 | A4 | d5 | ||||||
| 7 | P5 | d6 | ||||||
| 8 | A5 | mi6 | ||||||
| 9 | ma6 | d7 | ||||||
| 10 | A6 | mi7 | ||||||
| 11 | ma7 | d8 | ||||||
| 12 | A7 | P8 |
Example 16. Enharmonic equivalence of intervals.
Intervallic enharmonic equivalence is useful when you come across an interval that you do not want to calculate or identify from the bottom note. We have already discussed one method for this situation previously, which was intervallic inversion. You may prefer one method or the other, though both will yield the same result. Example 17 reproduces the interval from Example 11. As you'll recall, there is no key signature for the bottom note (E𝄫), making identification of this interval difficult. By using enharmonic equivalence, however, we can identify this interval more easily, recognizing that E𝄫 is enharmonically equivalent with D and that A♭ is enharmonically equivalent with G♯. Now we can identify the interval as an A4 (augmented fourth), using the key signature of the enharmonically equivalent bottom note (D).
- Lindley, Mark, revised by Murray Campbell and Clive Greated. 2001. "Interval." Grove Music Online. https://doi.org/10.1093/gmo/9781561592630.article.21263.
- McGrain, Mark. 1986. Music Notation. Boston: Berklee Press.
- Roemer, Clinton. 1985. The Art of Music Copying: The Preparation of Music for Performance, 2nd edition. Sherman Oaks: Roerick Music Company.
- Thompson, William Forde. 2013. "Intervals and Scales." The Psychology of Music, ed. Diana Deutsch: 107–40.
- Specific Intervals (musictheory.net)
- Interval Introduction (Robert Hutchinson)
- Intervals (Hello Music Theory)
- Diminished and Augmented Intervals (Open Textbooks)
- Diminished and Augmented Intervals (Robert Hutchinson)
- Compound Intervals (Hello Music Theory)
- Interval Inversion (musictheory.net)
- Interval Ear Training (musictheory.net)
- Interval Ear Training (Tone Dear)
- Interval Ear Training (teoria)
- Interval "Songs for Identification (Miami Date College)
- Interval Identification (musictheory.net)
- Keyboard Interval Identification (musictheory.net)
- Interval Identification, pp. 1–4 (.pdf), (.pdf, .pdf, .pdf), pp. 3–6 (.pdf)
- Interval Identification and Construction, pp. 18–19 (.pdf)
- Interval Construction (.pdf), p. 14, 19–21 (.pdf)
- Compound Intervals, pp. 15–17 (.pdf)
- Writing a Mix of Compound and Simple Intervals, pp. 1–2 (.pdf)
- Inverting Intervals (.pdf)
- Intervals A (.pdf, .mscz). Asks students to write and identify intervals by quality and size.
- Intervals B (.pdf, .mscz). Asks students to write and identify intervals by quality and size.
- Intervals C (.pdf, .mscz). Asks students to write and identify intervals by quality and size.
- Intervals D (.pdf, .mscz). Asks students to write and identify intervals by quality and size, identify and write interval inversions, and analyze a melody using intervals. Treble/bass only. Worksheet Playlist
- Intervals E (.pdf, .mscz). Asks students to write and identify intervals by quality and size, identify and write interval inversions, and analyze a melody using intervals. Treble/bass only. Worksheet Playlist
- Major, Minor, and Perfect Intervals A (.pdf, .mscz). Asks students to write and identify major, minor, and perfect intervals only.
- Major, Minor, and Perfect Intervals B (.pdf, .mscz). Asks students to write and identify major, minor, and perfect intervals only.
- Diminished and Augmented Intervals A (.pdf, .mscz). Asks students to write and identify diminished and augmented intervals only.
- Diminished and Augmented Intervals B (.pdf, .mscz). Asks students to write and identify diminished and augmented intervals only.
Materials in this chapter are from Open Music Theory, with the following revisions by Elizabeth Pauly: Call-out box and further explanations in "The Major Scale Method"; the addition of "Quick Tip for Identifying Interval Size"; the directions for simplifying intervals in "Compound Intervals"; adding the heading "Rule of Nine" to call attention to the process of intervallic inversion; and "A Variation of the White Key Method".
A type of binary form where the material at the start of reprise 1 returns somewhere near the middle of reprise 2. Both appearances of that repeated music are expected to be in the home key.
A variation on the 12-bar blues progression. Typically composed of four four-bar phrases, usually two iterations of tonic, followed by subdominant and dominant. The final phrase may or may not end with a turnaround.
A section of a work that bears repeat signs, like either of the parts of a binary form.
